Direct Variation

In these lessons, we will learn about direct variation and how to solve applications that involve direct variation.

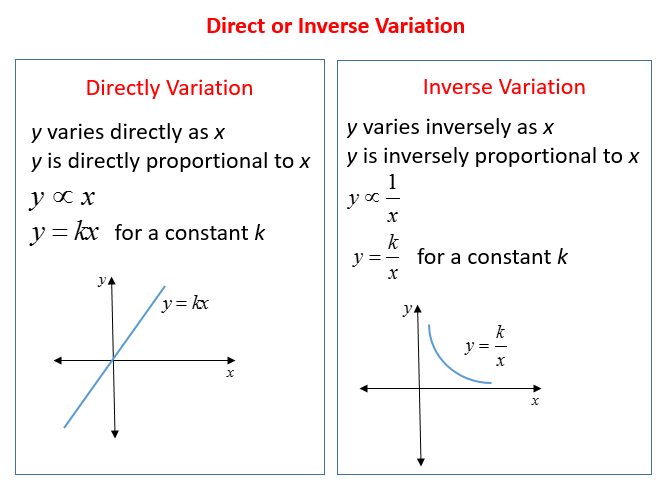
The following diagrams show Direct Variation and Indirect Variation. Scroll down the page for examples and solutions.

What Is Direct Variation?

There are many situations in our daily lives that involve direct variation.

For example, a worker may be paid according to the number of hours he worked. The two quantities x (the number of hours worked) and y (the amount paid) are related in such a way that when x changes, y changes proportionately such that the ratio remains a constant.

We say that y varies directly with x. Let us represent the constant by k, i.e.

or y = kx where k ≠ 0

If y varies directly as x, this relation is written as y ∝ x and read as y varies as x. The sign “ ∝ ” is read “varies as” and is called the sign of variation.

Example:
If y varies directly as x and given y = 9 when x = 5, find:
a) the equation connecting x and y
b) the value of y when x = 15
c) the value of x when y = 6

Solution:
a) y ∝ x i.e. y = kx where k is a constant
Substitute x = 5 and y = 9 into the equation:

b) Substitute x = 15 into the equation
y = = 27

c) Substitute y = 6 into the equation

Example:
The cost of a taxi fare (C) varies directly as the distance (D) travelled. When the distance is 60 km, the cost is $35. Find the cost when the distance is 95 km.

Solution:
C ∝ D i.e. C = kD, where k is a constant.
Substitute C = 35 and D = 60 into the equation
35 = 60k ⇒ k =

Therefore, C = D
Substitute D = 95 into the equation: C = 55.42
The cost for 95 km is $55.42

How To Define Direct Variation And Solve Direct Variation Word Problems?

Some examples of direct variation problems in real life:

• The number of hours you work and the amount of your paycheck.
• The amount of weight on a spring and the distance the spring will stretch.
• The speed of a car and the distance traveled in a certain amount of time.

The following statements are equivalent:

• y varies directly as x
• y is directly proportional to x
• y = kx for some constant k

What Is The Direct Variation Formula?

A direct variation is a linear equation that can be written in the form y = kx , where k is a nonzero constant. The number k is called the constant of proportionality or constant of variation.

Graphically, we have a line that passes through the origin with the slope of k.

Examples:

1. y varies directly with x. y = 54 when x = 9. Determine the direct variation equation and then determine y when x = 3.5
2. Hooke’s Law states that the displacement, d, that a spring is stretched by a hanging object varies directly as the mass of the object. If the distance is 10 cm when the mass is kg, what is the distance when the mass is 5 kg?
3. y varies directly with x. y = 32 when x = 4. Determine the direct variation equation and then determine y when x = 6

How To Determine A Direct Variation Equation From The Given Information And Then Determine y With A Given Value Of x?

Example: y varies directly with x. Given that y = 6 when x = 30, determine the direct variation equation and then determine y when x = 8.

Real Life Example Of A Direct Variation Problem

Example:
The total cost of filling up your car with gas varies directly with the number of gallons of gasoline that you are purchasing. If a gallon of gas costs $2.25, how many gallons could you purchase for $18?

Other Forms Of Direct Variation

The area A of a circle of radius r is given by the equation A = pr 2 , where p is a constant

In this situation, A is not directly proportional to r but A is directly proportional to r 2 . We say that ‘A varies directly as the square of r ’ or A ∝ r 2 .

Example:
Given that y varies directly as the cube of x and that y = 21 when x = 3, calculate the value of y when x = 8.

Solution:
y ∝ x 3 that is y = kx 3 where k is a constant

Substitute x = 3 and y = 21 into the equation:
21 = k(3 3 ) ⇒ k =

The following video gives some practical examples of direct variation and indirect/inverse variation.

How To Solve Word Problems Involving Direct And Inverse Variation Squared?

Examples:

1. On planet X, an object falls 18 feet in 2 seconds. Knowing that the distance it falls varies directly with the square of the time of the fall, how long does it take an object to fall 29 feet? Round your answer to three decimal places.
2. The Intensity, I, of light received from a source varies inversely as the square of the distance, d, from the source. If the light intensity is 4-foot candles at 11 feet, find the light intensity at 13 feet.

Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.